
Apolonio de Perga

Karen ortiz



¿Quien Fue?
(Apolonio de Perga o Perge; 262 a.J.C. - 190 a.J.C.)
Antonio de Perga nació en Alejandría aproximadamente en el año 262 a. C. dedicó su labor en las áreas de astronomía, geometría y matemáticas de la Escuela de Alejandría, siendo reconocido ampliamente por su tratado de las cónicas y de las curvas planas y la cuadratura de sus áreas. Acuñó los términos elipse, hipérbola y parábola.
En esta importante obra de Apolonio de Perga se encuentran avances de gran significado para los campos de aerodinámica y astronomía, así como de otras áreas a las cuales se dedicaba.
Inspirado en los académicos René Descartes e Isaac Newton, Apolonio tomó los tratados de ambos para apoyar sus avances tecnológicos a futuro.
Murió a la edad de 48 años en Alejandría, Egipto, en el año 190 a. C. se desconocen las causas.



Para muchos, utilizaba un lenguaje geométrico moderno, por ello, aun en la actualidad, los aportes de Apolonio de Perga han representado un valioso recurso en el campo de la geometría analítica.
Sus extensos trabajos sobre geometría tratan de las secciones cónicas y de las curvas planas y la cuadratura de sus áreas. Acuñó los términos elipse, hipérbola y parábola, que responden a las respectivas propiedades matemáticas de estas tres funciones. También explicó el movimiento de los planetas según la teoría de los epiciclos.
Sabemos que obtuvo una aproximación de pi entre 22/7. Consideró un solo cono y hace variar la oblicuidad del plano que lo corta. De esta manera obtuvo como curva fundamental la parábola cuya ecuación es y2 = 2pix. Las otras dos curvas las caracteriza por: y2<2pix, que equivale a la hipérbola ("exceso").
En "On the Burning Mirror" mostró que rayos de luz paralelos no caen a un foco en un espejo esférico (como ha sido previamente pensado) y discutió las propiedades focales de un espejo parabólico. Además, fue fundador de la astronomía matemática griega, la cual usó modelos geométricos para explicar la teoría planetaria. Se le atribuye la invención del reloj solar.
Aportaciones matemáticas



Historia de las Cónicas
Conocido como "El gran geómetra", su famoso libro "Secciones Cónicas" introdujo los términos: parábola, elipse e hipérbola espiral. Ideó el tornillo, inventado en el año 200 AC. El invento se generó a partir del desarrollo de la geometría de la hélice espiral.
Creó los cimientos de la geometría a través de un compendio de 8 libros titulados Tratado de las cónicas. Los libros del 1 al 4 no contienen material original pero introducen las propiedades básicas de cónicas que fueron conocidas por Euclides, Aristóteles y otros. Los libros del 5 al 7 son originales; en estos discute y muestra como muchas de las cónicas pueden ser dibujadas desde un punto. Da proposiciones determinando el centro de curvatura lo cual conduce inmediatamente a la ecuación cartesiana del desarrollo de la evolución. El libro número 8 de "Secciones Cónicas" está perdido, mientras que los libros del 5 al 7 sólo existen en traducción arábiga.


Cónicas
Las cónicas son figuras geométricas que pueden definirse como lugares geométricos en el plano.
Una sección cónica se ingresa como una ecuación cuadrática en x e y. Se pueden emplear en la ecuación, variables previamente definidas (números, puntos, vectores).
A continuación, verás las cuatro más importantes.
La circunferencia es la sección producida por un plano perpendicular al eje.
La circunferencia es un
caso particular de elipse.
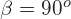


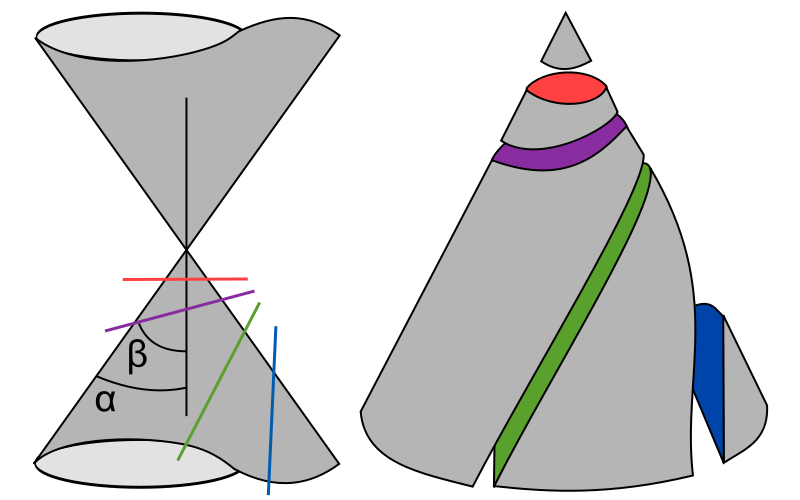
La elipse es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, que no sea paralelo a la generatriz y que forme con el mismo un ángulo mayor que el que forman eje y generatriz.
La elipse es una curva cerrada.
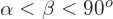
La parábola es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, siendo paralelo a la generatriz.
La parábola es una curva
abierta que se prolonga
hasta el infinito.



La hipérbola es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, formando con él un ángulo menor al que forman eje y generatriz, por lo que incide en las dos hojas de la superficie cónica.
La hipérbola es una curva
abierta que se prolonga indefinidamente y consta de
dos ramas separadas.


Ejemplo
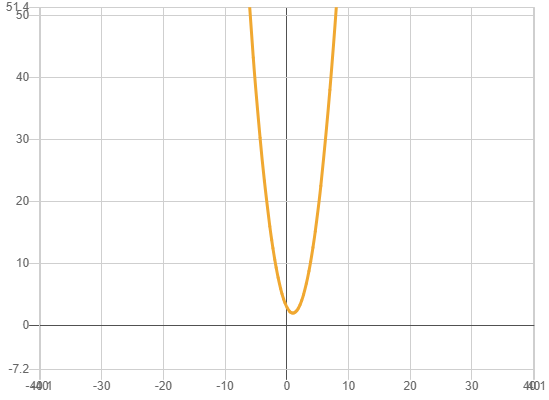
y=x^(2)-2x+3
La ecuación y = x 2 - 2x + 3 corresponde a una parábola de eje vertical x = 2 2 = 1 y ramas hacia arriba, ya que el coeficiente de x 2 es positivo.

Fuentes
- Diego. (2021). Apolonio de Perga. Matemáticas desde CERO. https://matematicasdesdecero.com/matematicos-destacados/apolonio-de-perga/
- Biografia de Apolonio de Pérgamo. (s. f.). https://www.biografiasyvidas.com/biografia/a/apolonio_de_pergamo.htm
- De La Oliva Estrella Moreno Y Otros, V. M. M. E. R. C. (s. f.). Biografía de Apolonio de Perga (Su vida, historia, bio resumida). https://www.buscabiografias.com/biografia/verDetalle/9147/Apolonio%20de%20Perga
- Marta. (2021, 1 octubre). Todo sobre las conicas | Superprof. Material Didáctico - Superprof. https://www.superprof.es/apuntes/escolar/matematicas/analitica/conica/conicas.html
- https://ocw.unizar.es/ocw/pluginfile.php/72/mod_label/intro/u5conreto.pdf

¡Gracias!